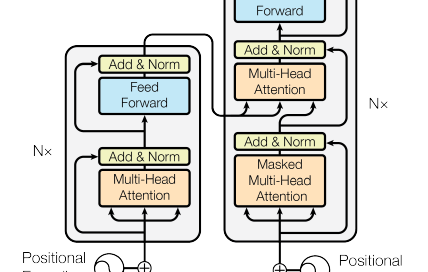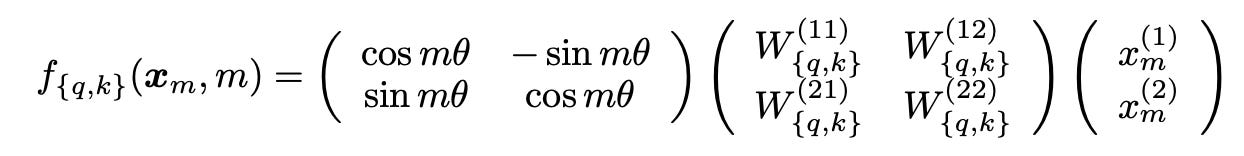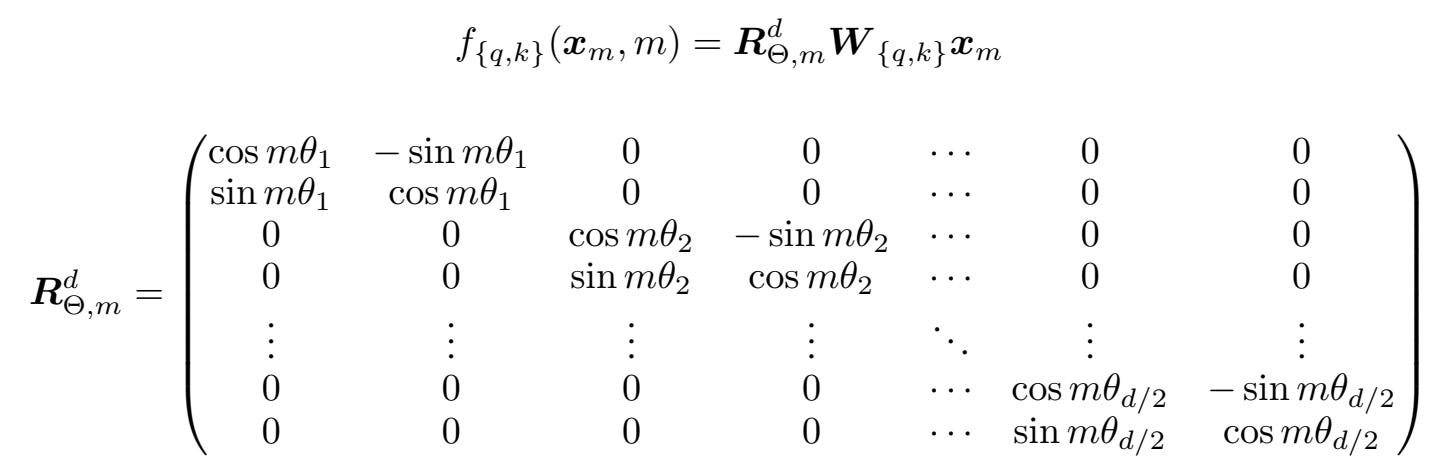
“Attention is All You Need”
– Google researchers in 2017
Amongst the many mysteries of modern deep learning, the remarkable success of attention is one of my favorites. There’s something about it that just seems like it shouldn’t quite work as well as it does. Nevertheless, for all the hate, and attempts over many years to replace it, it is still around!
Let’s dig into it a bit today.
We start with a simple but enduring problem – sequence modeling. Simple and infinitely expressive.
Sure, there are some details around BPE tokenization and hard-coded semantic rules that we humans dearly depend on and that deep learning researchers so despise, but its a hack thats worked so far, so we shrug and leave that for another day, as we have for the past many years.
We are working with sequences of integers, each integer mapping in some arbitrary manner to its own class embedded with rich information. Each integer value associated with its own concept and all of its deep context.
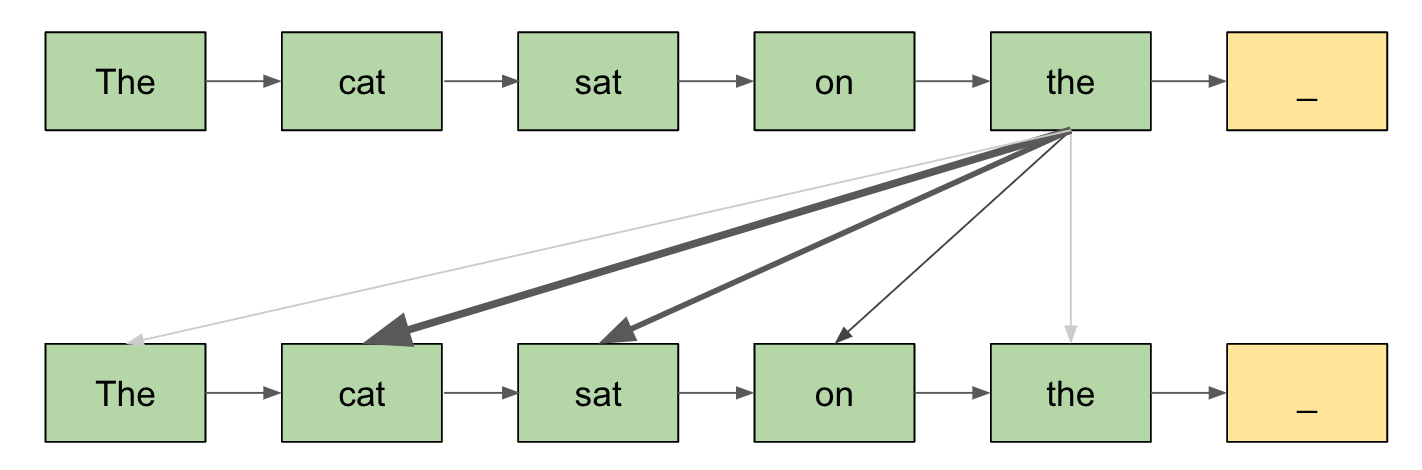
We find ourselves in a setting where the relationships between the elements in sequences are, though not entirely trivial, still relatively simple. Preposition elements pointing to elements before them, pronoun elements map back to noun elements in sometimes complex ways, but still mostly simple enough that these can be deduced from context. Adjective elements adjust the nuance of subsequent elements. Simple rules, but nevertheless, a large slew of them, too many to write down, and sufficiently diverse that general learning methods must be used.
In comes Attention. Or, to be specific, Self-Attention.
Attention models both content and position. How content is modeled – QKV vectors – is better understood than positional information. It is also more intuitive. Different parts of the embedding vector model different concepts such as punctuation, time, language, etc. The value matrices pull out subsets of these embedding spaces to model specific concepts, the key matrices pull out related concepts necessary to index this content, and query matrices pull out the subset of the embedding space that determine what indexed content to retrieve.
Side note: Concept capacity in d-dimensional spaces
Some justification for why QKV vectors are capable of modeling all of human language – at the bare minimum, they can just subsample the embedding concept space that is the d-dimensional unit sphere, and d-dimensional spheres can fit a lot of information! We can assume we are working on unit spheres due to the layer norms so commonly used today enforcing norm-agnosticism in modern day Transformers.
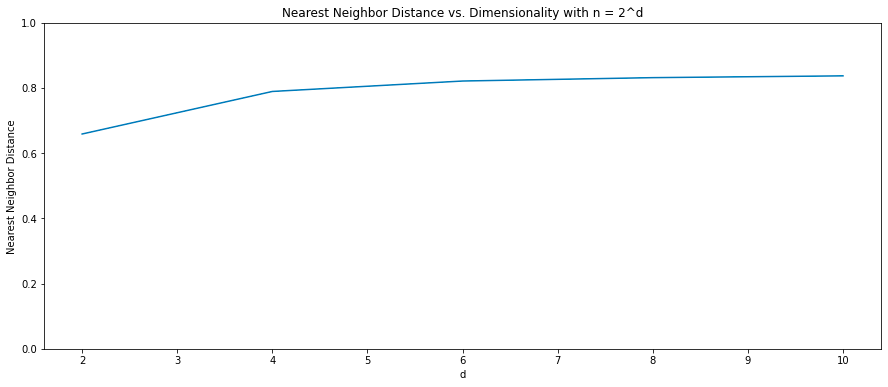
In d-dimensions, as d increases, one can fit many concepts. Let’s quickly contemplate how many. Suppose each concept is it’s own vector in this d-dimensional sphere. To differentiate concept vectors, each vector must have some minimum cosine distance, let’s call this x for now, from all other vectors. An upper bound on the number of vectors can be calculated by looking at the total d-dimensional volume occupied by each vector, i.e. at distance x or less.
The d-volume taken up by a single unit vector u is the space of the d-sphere with distance x or less from this vector is
since we must allocate x distance of any competing vector in the unit direction u, and the remaining 1-x is allocated over the remaining d-1 dimensions (since vectors are unit norm). If we fix x=0.5 for now (x is clearly not the dominating factor as the base of an exponential), we see we can fit roughly O(2^d) concepts in a d-sphere.
Running a simulation confirms this – modulo constants, mean cosine distance between vectors and their nearest neighbor appears to plateau as you increase d and set number of concept vectors to 2^d.
This bodes well for deep learning. Usually parameter count grows as O(d^3) as you need to scale feedforward matrices as O(d^2) and the number of layers proportional to d. Concepts growing exponentially in d means that we win as we scale up. Yes, costs go up superlinearly, but the capacity of our space grows even faster. Worth noting of course is that, with increasing complexity, total number of concepts to model probably grows exponentially too.
Position embeddings
Enough of concepts! The most fascinating part of attention is not this, but rather the often overlooked nature of how it handles positional information. As is commonly known, the model has no built-in concept of sequence order, unlike its predecessors RNNs and LSTMs, and the newer SSMs. To work around this, position information is embedded into the model by adding hard coded position vectors, either onto the initial embedding, or the QK vectors. Amazingly, this is sufficient for models to model positional information on contexts of up to millions of tokens!
These position embeddings are rich in information, and yet they are simple, man-made objects. The original position embedding vector from the Attention is All You Need (AIAYN) paper is constructed element-wise for a token at position pos by setting the value of each odd and even dimension i as follows:
Where the base frequency of each dimension is defined as:
People wiser than me may disagree, but when I first read AIAYN, I did not find it intuitive at all why these position embeddings should work at scale. Let’s first just grok what these embeddings are even doing.
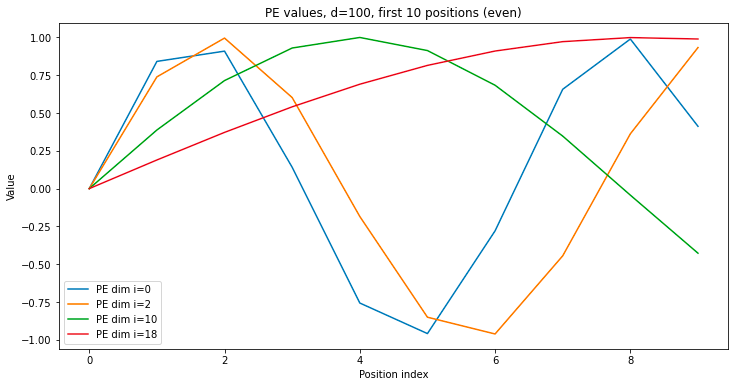
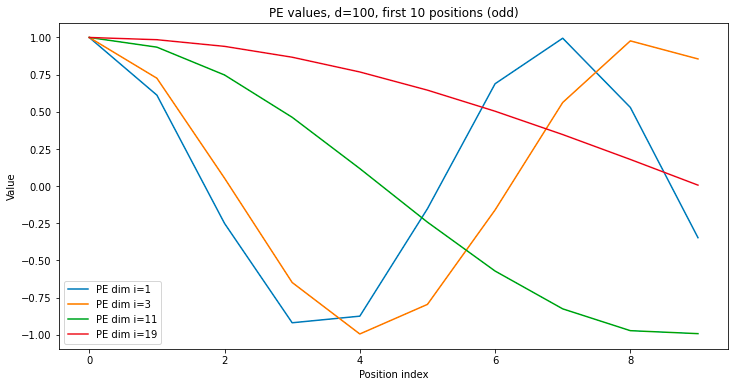
The overall structure of the position embedding is to group embedding dimensions into pairs, and for each one, to calculate the sin and cosine of the position index times some base frequency for that group. The base frequencies start of extremely large and shrink exponentially as you iterate through the groups. Let’s look at what these position embedding values look like as you scan across position index, for varying group indices.
As you scan across the position of a sequence (i.e. go from first token to the last token), the position embedding values oscillate rapidly for the smaller indices of the position embedding, and very slowly for the larger indices. The smaller indices are very sensitive to changes in position, while differences in value for the larger indices only appear at greater position distances. The smaller indices are useful for differentiating tokens at short distances from each other, while the larger indices are useful at long distances.
Digging into AIAYN position embeddings
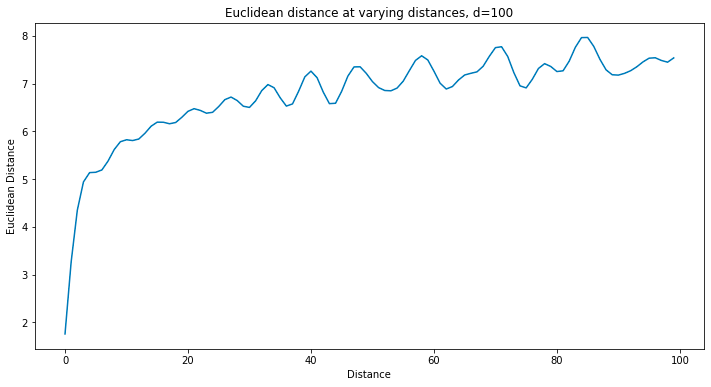
How much information is embedded within these position embeddings? Let’s take a look, starting with how well they can differentiate position indices. Each group i consists of a value sin(pos f_i) and cos(pos f_i) for base frequency f_i, so at distance k the squared Euclidean difference is
Wow that simplifies nicely. It’s entirely a function of distance! And the shape of the difference values exactly matches those of the values in the position embedding themselves (sinusoidal with frequency dependent on group index i). Adding this up across all groups i and you get something not analytical but still quite nice:
Let’s do a quick sanity check. Is it possible with these position embeddings to produce a QK mapping which “selects” (i.e. attends maximally to) the token at distance k away from the current one? Turns out that the answer is yes, as is expected and fortunate for us. First, let’s start with QK vectors of equal dimension to the embedding dimension. Then one can map each group linearly as follows:
And voila, you’ve reproduced the position embedding of the token at distance k away, which will thus have the highest dot product (attention) score. Compressing this into a smaller subspace can then be done more or less arbitrarily and you are likely to produce pretty good results.
Nice. These position embeddings seem to work. One can differentiate tokens and select positions in the attention mechanism. Unfortunately, these position embeddings are not perfect. We can see that the structure of these position embeddings are such that identifying the distance between two tokens requires comparing the values group-wise, since non-equal frequencies desynchronize rapidly, so comparing values across groups produces no clearly meaningful signal. This is bad for the attention mechanism – it’s clear how this can force the QK vectors to select quite simple mappings that just select subsets of the groups and map them into the same indices in the Q and K vectors. More complex interactions between dimensions in the QK mappings are discouraged. It would be ideal if this could be avoided. Thankfully, people thought of this and came up with improvements.
Modern position embeddings
A lot of position embedding approaches have been tried. GPT-1 through 3 used learned embeddings. GPT-4’s architecture is unknown. Nowadays, all open-source models use RoPE embeddings. These position embeddings are quite nice – they are added directly onto the QK vectors! This means that the QK mappings are free to extract and mix subsets of the embedding vector in an arbitrary manner, since position information is added post-hoc.
RoPE goes back to hardcoded sinusoidal values but with some modifications justified through elegant math. In short, every consecutive pair of values in the output of each QK mapping is once again treated as a group, and are rotated by some angle based on their position and the base frequency of that group.
The elegance of this approach is that (1) the embedding vectors themselves are undisturbed by positional information, (2) translation invariance – rotation of one vector at position m and another at n is equivalent to rotation at 0 and n - m.
It is clear that the same argument as before with additive position embeddings apply here, and as such selection of a token at distance k away can be produced just by setting the appropriate Q and K values before the position rotation, although this case is non-trivial since there are no biases in attention mechanisms and the input vectors to the QK mapping can be arbitrary, so one is not guaranteed to be able to fix the values one wants. My guess for why this doesn’t matter is that the embedding vector presumably learns some hardcoded constant values to help the network out.
Expanding context
One significant benefit of hardcoded position embeddings is that there is some underlying structure to the values added post QK mapping that one would hope that the attention mechanism would pick up. If this is the case, then one ought to be able to simply extend the context window beyond what the model was trained for and see natural interpolation and improved performance.
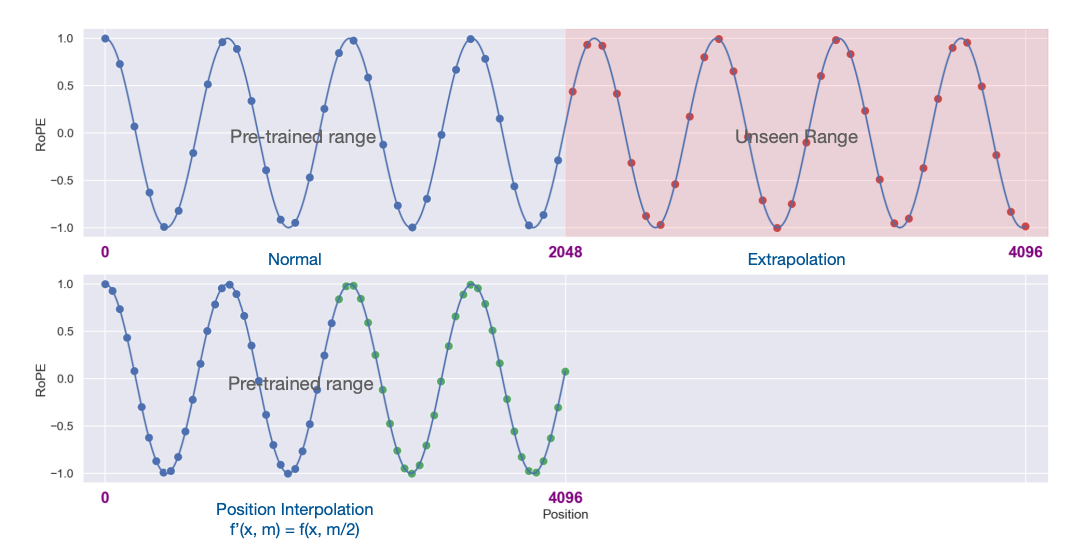
Unfortunately, this is not what happens by default. When one naively adds more context, one unfortunately tends to see Perplexity explode. There are a few hypothetical explanations, but the most common one is that the model never learns to ignore context with unseen position embeddings, so attention scores get messed up.
The easiest solution is Position Interpolation – simply drag out the position embeddings by reducing the base frequencies by a constant proportional to the increase in context length. This works ok, but requires a decent amount of re-training.
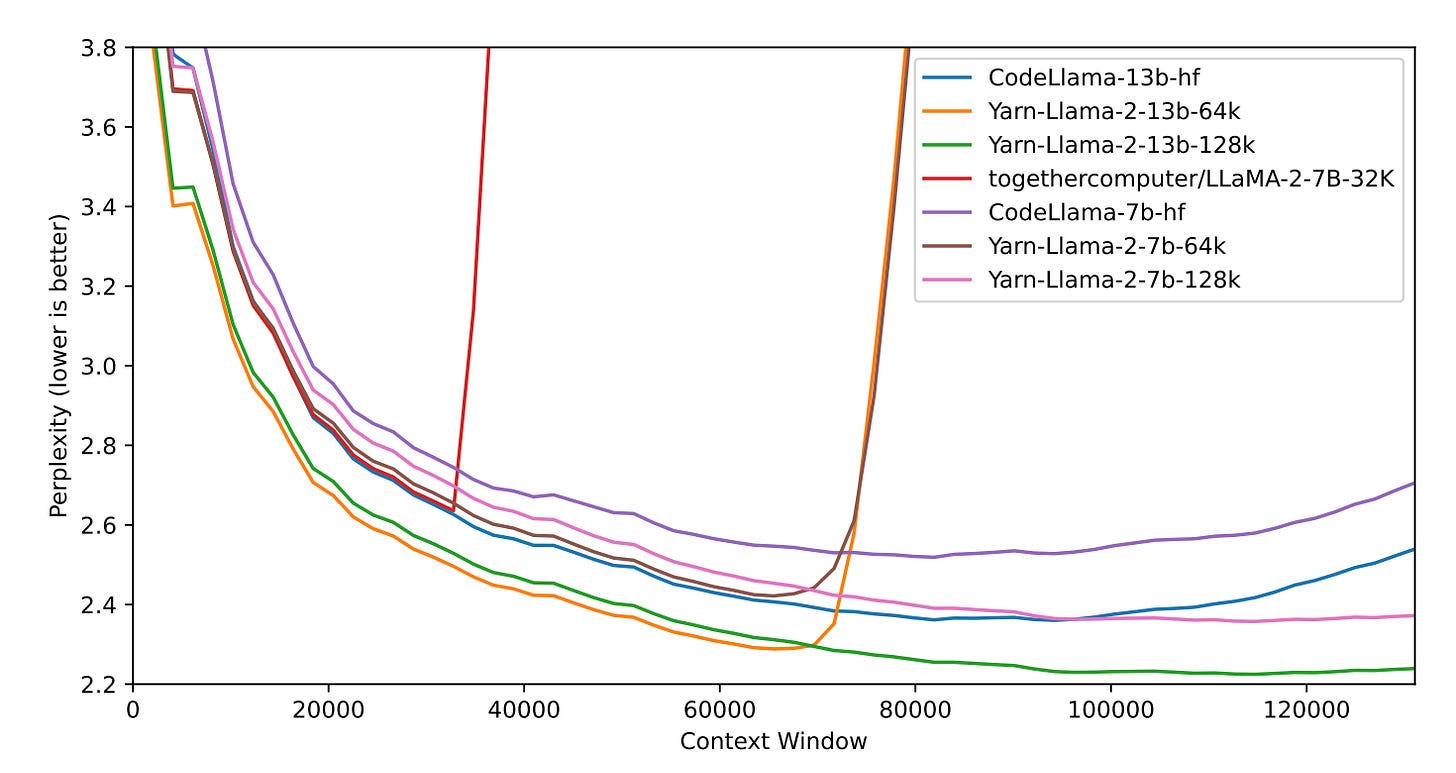
YaRN improves on this by recalling that some group indices focus on short-term position information (in particular the earlier indices) while others (the latter indices) focus on long-distance information. One only needs to worry about stretching the latter to improve long context performance. In addition, one must readjust the normalization constant in the softmax scoring of the attention mechanism to account for the increased number of tokens. I would go over the math here but the intuition and empirical results are robust enough that I find it worth skipping.
In either case, I find it interesting and a little ironic that the original motivation for hard-coded position embeddings was that the model would generalize beyond the context space it was trained on, and yet the only way people have been able to get them to generalize has been to “stretch out” the space it was trained on to cover more context.
Overall thoughts
People don’t spend enough time thinking about the position embeddings of Transformers. From all I can see, this is literally the main difference between Transformers and every other contending NLP model family – LSTMs, SSMs, convolutions, etc. Rather than hard-code sequential information into the very architecture of the model, the Transformer does something radical – it demotes the importance of position, stating “you are not important enough to be an intrinsic part of the architecture. We will only pay attention to you through the position embeddings you pass as input!”
Or perhaps, it says something else… that position is so important and complex that it must be promoted, that hard-coded architectural information is so limited that the model instead must learn the nature of positional relations by itself. I like this interpretation a lot. Language is incredibly complex. The fact that books have words that refer back to pages upon pages suggests that information flow is not very well behaved. It is not ordered sequentially. Perhaps we should not force our models to learn in this manner then.
This is one reason I am concerned for SSMs, despite all the hype around them right now. I would love to be proven wrong. It’s great to have competition, and many contending architectures. Nevertheless, sequential structure based around position feels intrinsically limiting to these models. You’re forcing it to understand the world with a restricted view. The O(n^2) attention penalty must be beaten yes, but perhaps it can be done without going back to the dark age of architecturally hard-coded positional information.
Perhaps this is a lesson we should extend to other parts of the Transformer… like… idk… the universally hated BPE tokenizer? 🙃
What’s next?
Infinite context. Jk. Increasing context length is definitely coming, but infinite context requires some dramatic changes, including getting rid of this business of naively extending the attention mechanism. Thankfully we can wait quite a bit – d-spheres store exponentially growing amounts of information, thus also exponential amounts of positional information. We can probably scale to context lengths in the millions with just existing attention techniques. Already at this scale we are struggling to find use cases that can make use of this context (while affording the computational cost).
That said, something feels wrong about this approach. The math here points to scaling being enough, that we can just expand the size of the QK vectors and exponentially grow our context capacity. Scaling always wins. But it feels wrong. It feels inelegant. As if some form of compression and retrieval, the way humans handle memories, ought to be necessary. Of course, this is a classic intuitive fallacy. Machines do not think the way humans do. Just because humans do things in a certain way does not mean machines must do so too in order to surpass us.
It’ll be interesting to see which is right in the long term – mathematics, or intuition.
(Code for all experiments can be found on my GitHub)